Je suis MAITRE de CONF en MATHS

https://m.youtube.com/watch?v=VtltD5Yt0h0&pp=0gcJCcEJAYcqIYzv

Si je veux comprendre une telle conf un jour, le seul chemin est de "backtracker" avec les mots-clés ?

Sinon je passerai bien vingt-cinq ans à 'escalader la montagne' à partir des bases, bases sur bases ?

Les personnes qui ont ce niveau à cet âge ont formément des capacités naturelles supérieures ? Peut-on vraiment se permettre de "griller" des étapes sans avoir fait des exercices sur CHAQUE notion, car il faut bien que le manuscrit de la thèse soit prêt avant la deadline

Le 05 juillet 2025 à 21:10:04 :
https://m.youtube.com/watch?v=VtltD5Yt0h0&pp=0gcJCcEJAYcqIYzv

Si je veux comprendre une telle conf un jour, le seul chemin est de "backtracker" avec les mots-clés ?

Sinon je passerai bien vingt-cinq ans à 'escalader la montagne' à partir des bases, bases sur bases ?

Les personnes qui ont ce niveau à cet âge ont formément des capacités naturelles supérieures ? Peut-on vraiment se permettre de "griller" des étapes sans avoir fait des exercices sur CHAQUE notion, car il faut bien que le manuscrit de la thèse soit prêt avant la deadline

Prenons la question dans l'autre sens : pourquoi voudrais-tu comprendre cette conf ?

Visiblement, elle porte sur des choses qui "te dépassent", au sens où tu ne comprends pas de quoi il s'agit donc, en particulier, ne peux pas saisir pourquoi ce serait intéressant. Ca peut sembler assez vain de se donner un objectif très ambitieux de compréhension de sujets de pointe quand on n'a pas l'éducation permettant de ressentir personnellement que ces sujets te parlent et t'intéressent vraiment.

Je ne dis pas ça sur le ton de "tu as tort d'avoir cet instinct". Je te suggère seulement, cet instinct étant là, de prendre ensuite le temps de l'analyser de façon critique et lucide.

L'instinct de vouloir améliorer sa compréhension, d'avoir un appétit d'inconnu, il est globalement sain. Mais quand il s'agit de faire des choix pour orienter ses efforts, il convient de prendre en compte l'intérêt concret que représente à tes yeux ces concepts, le temps que ça prend de les acquérir, etc. Et de ne pas tomber dans la collectionnite. J'arguais ici que vouloir tout savoir sur tout est un mauvais rapport à la connaissance :
https://www.jeuxvideo.com/forums/message/1184014264

Normalement, si on en vient à avoir la maîtrise de ces sujets, c'est plutôt (ou ça devrait être) qu'on a eu un cursus où les choses se sont faites de proche en proche, par glissement successif. Et un jour, on se retrouve au stade où on maîtrise ces questions.

Mais bon, admettons qu'on veuille tout de même tenter la chose. Dans ce cas, voici trois pistes :

1. tâtonner à essayer de "joindre les deux bouts", tantôt en apprenant les bases, tantôt en backtrackant depuis la destination finale ;
2. demander à un expert du sujet de nous vulgariser la chose et de nous baliser le chemin ;
3. suivre la voie que suivent à peu près tous les mathématiciens professionnels, à savoir faire une licence puis un master puis un doctorat.

Bref, oui, pour maîtriser ce genre de choses, tu en as probablement non pas pur 25 ans mais pour 5 à 10 ans post-bac. C'est le temps que ça prend à ceux qui en font leur métier. Après, si le but est juste d'en avoir une vision vulgarisée pour superficiellement comprendre certaines choses, ça peut s'acquérir plus vite. Mais bon, ça demandera déjà des efforts conséquents et on peut se demander si on a vraiment envie de faire des efforts soutenus pendant des mois pour n'avoir à la fin qu'une vision superficielle, quasi-vulgarisée.

Il faut bien se dire que telle personne qui a une expertise de ouf dans un domaine A l'a fait au prix d'efforts longs et soutenus, qui font qu'on n'est pas simultanément spécialiste des domaines B et C. Il ne faut pas, chaque fois qu'on voit une vidéo youtube inspirante, se dire "je veux faire ça dans ma vie", sinon tu entretiens la mégalomanie de vivre mille vies en une. En définitive, tu ne vivras aucune de ces mille vies à fond. On en revient au fait que vouloir tout savoir sur tout est un mauvais rapport à la connaissance.

Après, bien sûr, ta demande n'était pas absurde du tout. Notamment, dans d'autres sujets, les compétences requises pour lire et globalement comprendre un article sont beaucoup moins exigeantes que celles qu'il faut pour rédiger un tel article de recherche. Mais les maths en général, et la géométrie algébrique en particulier, sont une discipline âpre et technique : pour cette discipline, même lire requiert une longue formation. Car non seulement il y a du jargon technique mais il y a un aspect abstrait/précis/conceptuel, avec des poupées russes de concepts qui en renferment d'autres... bref, un tel aspect qui fait que c'est chaud

Quant à ta dernière question : si on suit un cursus mathématique jusqu'au doctorat, il n'y a pas grand chose de très surprenant à être capable de gérer des maths de recherche de haute volée à 25 ans. Après, est-ce qu'il faut des "capacités naturelles supérieures" pour arriver jusqu'au doctorat ou pour faire une bonne thèse : plutôt que de sortir des préjugés à ce propos, je vais assumer mon ignorance.

Peut-on vraiment se permettre de "griller" des étapes sans avoir fait des exercices sur CHAQUE notion, car il faut bien que le manuscrit de la thèse soit prêt avant la deadline

Ca dépend de quelles notions jouent un rôle central ou non dans ce que tu fais. Les notions centrales, tu dois te les être appropriées intimement. Les autres, c'est bien si c'est le cas mais pas dramatique si ce n'est pas le cas. Notamment, la phrase précédente contient l'information que c'est bien si c'est le cas : en effet, prendre l'habitude de bien comprendre ce qu'on apprend est une bonne habitude en soi, et par ailleurs fait gagner un recul général qui est bénéfique à terme.

Par ailleurs, précision dans mon post précédent. Quand je dis :

Il faut bien se dire que telle personne qui a une expertise de ouf dans un domaine A l'a fait au prix d'efforts longs et soutenus, qui font qu'on n'est pas simultanément spécialiste des domaines B et C.

je ne dis pas qu'il est impossible d'avoir plusieurs spécialités au sein des maths. Je voulais plutôt dire "tu ne vas pas être chef étoilé et médaillé olympique et biologiste renommé". A un moment, t'as un nombre fini de points de compétence à poser et tu décides comment tu les répartis. Avec 20 points, tu peux soit en mettre 20 sur un domaine, soit 10+10, soit 10 sur un domaine puis 10 domaines à 1, etc

En fait, quand on réfléchit un peu autour, la question de petitcahier soulève un point intéressant, notamment dans la vulgarisation scientifique. Il s'agit de faire passer des idées, et pourquoi pas des vocations, du monde des spécialistes vers tout le monde.

Toutefois, pour que le travail soit bien fait, il faut qu'il soit bien fait. Il ne suffit pas qu'une idée passe, il faut que l'idée reçue soit en effet proche de celle à transmettre, qu'on ne fasse pas passer des vessies pour des lanternes.

Idéalement, après une vulgarisation de qualité, on comprend raisonnablement bien ce qu'on croit comprendre, on sait ce qu'on ne maîtrise pas et, si on est enthousiaste, on saurait expliquer pourquoi. C'est un art difficile. Un art qui a moins de valeur et qui est moins difficile (sans être particulièrement facile), c'est celui de "faire rêver sans ces scrupules intellectuels".

A mon sens "faire rêver avec scrupules intellectuels" > "vulgarisation scrupuleuse qui ne fait pas rêver" > "faire rêver sans scrupules"

Ce que je viens de dire sur les idées s'applique également au niveau des vocations. Un enfumeur peut faire rêver quelqu'un ou encore faire miroiter "waow, t'as vu comme je suis classe à bosser sur tel sujet plus profond que l'univers lui-même". Mais le vulgarisateur ultime, il t'aidera à poser des choix de vie et d'efforts éclairés, en ne négligeant pas toutes les considérations pragmatiques, réalistes. Bref, il nourrira ta vision des choses de façon féconde.

Pourquoi ya pas d'aide visuelle en cours de math pour visualiser les théorèmes et objets comme en physique, sans visualiser les trucs les élèves comprennent absolument rien, ils font juste des calculs et des demonstrations sans comprendre

Et pourquoi ya pas dintro historique pour comprendre pourquoi tel ou tel outil à été créé et son utilité pratique

Le 05 juillet 2025 à 23:28:34 :
Pourquoi ya pas d'aide visuelle en cours de math pour visualiser les théorèmes et objets comme en physique, sans visualiser les trucs les élèves comprennent absolument rien, ils font juste des calculs et des demonstrations sans comprendre

Et pourquoi ya pas dintro historique pour comprendre pourquoi tel ou tel outil à été créé et son utilité pratique

Tu penses à un niveau d'enseignement précis ou bien est-ce un peu général ? Lycée ? Licence ? Autre ?

Concernant les aides visuelles, certains sujets s'y prêtent plus ou moins que d'autres. Et ensuite, ça dépend des enseignants que tu as.

Par ailleurs, à terme, l'une des utilités des maths est de savoir manipuler le raisonnement abstrait. Le mot "abstrait" n'est pas à prendre ici en un sens négatif, comme une absence de "concret" qui serait positif. Quand un concept est abstrait, ça signifie que c'est une espèce de "concept pur" qui, du fait qu'il est "assez immatériel", est susceptible de s'appliquer dans des situations très variées. Il importe à un moment que cette capacité d'abstraction soit transmise car

1. comme je viens de le dire, ça a une vertu unificatrice (gérer des situations très variées d'un seul coup),
2. du point de vue logique, quand on raisonne mathématiquement plutôt qu'en référence à un référent concret, on sait très exactement quelles hypothèses on fait sur ce qu'on étudie (or, scientifiquement, c'est précieux d'avoir un champ du savoir où toute hypothèse est explicite).

Ce que je viens de dire est là non pour s'opposer à ton propos mais pour le compléter. Je dis qu'il faut à terme développer l'abstraction. Je ne dis pas que, pour ce faire, les référents visuels sont proscrits. Je ne le pense pas, d'ailleurs. Mais il me paraît intéressant aussi d'apprendre à se passer de ces référents.

Par ailleurs, certains concepts mathématiques se prêtent moins que d'autres à des représentations visuelles aidantes.

Enfin, les différents pays n'enseignent pas forcément les maths de la même façon, en insistant sur les mêmes choses. Démêler pourquoi les maths sont comme ça en France en 2k25 dépasse probablement mes compétences. Il faudrait probablement retracer l'histoire de l'enseignement des maths depuis la Révolution jusqu'aux maths modernes puis à divers courants de pédagogie/didactique...

Pour l'intro historique, j'imagine que la raison est possiblement un manque de temps, de compétence historique, ou des deux. Certains enseignants y font allusion.

Quand on enseigne un concept, c'est qu'il est jugé intéressant. Toutefois, il n'est pas systématique qu'on puisse, de façon pleinement convaincante, expliquer son intérêt dès le moment où on l'introduit. Idéalement, à défaut de donner une motivation pleinement convaincante, il serait bon à minima d'esquisser les possibilités ouvertes par le cours qu'on va commencer. Du genre : Le but de ce cours est de commencer la théorie de Blabla. Avec une théorie avancée de Blabla, on peut résoudre des problèmes tels que [lister quelques problèmes qui sont assez naturels pour intéresser les élèves]

L'approche historique peut aussi être une façon de motiver. Le côté "narratif" d'avoir des personnes, ça peut capter l'intérêt. Après, ça capte l'intérêt plus sur "raconter une petite histoire", ça ne va pas forcément consolider très fortement l'intérêt pour la science elle-même, ni pour l'Histoire comme discipline scrupuleuse. Et par ailleurs, on continue de s'exposer au problème précédent : les questionnements antérieurs du point de vue historiques peuvent être plus compliqués que ce qu'on s'apprête à aborder.

Un truc qu'on observe assez fréquemment en science, c'est "on part de certaines choses, on les comprend confusément, et à la fin, ça y est, on a capté : on a de belles définitions et une belle théorie". Le pari fait tacitement dans l'enseignement standard, en ignorant le cheminement historique, c'est qu'on a alors intérêt à zappé la phase de tâtonnement intermédiaire. Cela a un gros avantage et un gros inconvénient. Le gros avantage, c'est que ça permet le "progrès" : si on s'autorise à prendre des raccourcis, eh bien une notion qui prenait 3 ans à acquérir peut désormais s'acquérir en 1 an. Le gros inconvénient, c'est qu'en sautant directement à la destination finale, on perd le sentiment que ce qu'on fait est naturel. Ca semble tombé du ciel. Un très bon enseignant cherche généralement à trouver une façon de considérablement amenuiser l'inconvénient sans trop sacrifier l'avantage.

Le 05 juillet 2025 à 23:43:23 :
Et aussi pourquoi introduire la théorie des groupes avec un ensemble de nombre (R,+) ou (C,+) alors que c'est absolument pas le but, alors qu'un groupe c'est un ensemble de transformations qui décrivent une symmetrie

100% d'accord avec toi

Le protype de groupe, c'est Z/nZ (en tant que groupe de rotations sur une horloge) ou le groupe symétrique.

R et C sont des prototypes de corps (ou d'anneaux).

Mais après, en vrai, je pense que c'est plutôt comme ça que ça se passe :

On est dans un cours où on veut introduire les anneaux et les espaces vectoriels. Pour ne pas donner toute la définition d'un coup dans la gueule, on va commencer par ne prendre qu'une seule opération, celle qui est commune aux deux. Et il se trouve que ça donne les "groupes abéliens". Donc on étudie ça. En gros, c'est une préthéorie, pas spécialement intéressante une fois qu'on est niveau master, mais c'est une introduction simultanée aux anneaux, aux espaces vectoriels et aux groupes.

Par contre, si tu fais un cours où tu bosses avec des groupes pas supposés abéliens, alors il est essentiellement obligatoire que tu fournisses un exemple de groupe intéressant pas abélien. Dans 95% des cas, j'imagine que tu fourniras le groupe symétrique. Et là pour le coup, ça va à fond dans le sens de ce que tu dis : "symétrie" est jusque dans le nom du groupe

Enfin bon, R et C comme groupes, c'est pas full débile. Déjà, on s'appuie sur quelque chose de connu et qui, de fait, est bien un groupe. Et par ailleurs, ça encode bien les translations en dimension 1 et 2. On pourrait mettre R^n à ce tarif-là : mathématiquement, ce serait naturel mais il n'y a peut-être plus le côté "s'appuyer sur quelque chose où l'addition a été manipulée beaucoup de fois".

Après, je suis d'accord, insister trop pesamment dessus risque d'engendrer des croyances du genre "un groupe, c'est un pré-anneau". A posteriori, ce n'est pas la bonne façon de penser ce qu'est un groupe, du moins pour un géomètre. Reste à voir toutefois si cette croyance est dommageable ou non. Si jamais une trajectoire efficace pour édifier un étudiant passe par des phases de croyances à réviser (surtout que là il ne s'agit pas de dire un truc faux, seulement d'un changement d'emphase), ça peut s'envisager, faut voir au cas par cas et sur ce qui fonctionne en pratique et à long terme.

Groupe ca doit être au minimum introduit par un groupe de matrices , comme ca au moins c'est déjà une représentation linéaire de groupes plus intéressants et exhibe des symétries, et ca a relation avec des transformations géométriques sur R3 genre rotations SO(3)

Pour les représentations géométriques, on a beau dire que non faut des définitions abstraites parce que l'objet couvre des cas abstraits mais le cerveau humain est fait ainsi, il est visuel, pour moi vaut mieux avoir la base géométrique pour un raisonnement et compréhension rapide puis étendre au cas abstrait plutôt que de démarrer abstrait dés le début et continuer abstrait, ca aide pas l'élève, le prof il a le temps de chercher dans les bouquins pour bien comprendre, l'élève a pas ce temps, il doit vite comprendre pour les exams et passer a autre chose

Et c'est aussi bon pour la carte mentale, la carte mentale humaine fonctionne visuellement pour connecter les concepts entre eux

Et pour l'introduction des outils et théories faut obligatoirement comprendre le but, sans but ya 0 motivation

c'est Dommage, le but est généralement très intéressant et pousserais l'élève a se dire "bah tient en apprenant ca je pourrais faire ce truc", c'est beaucoup plus intéressant

Aussi, les scénarios ou le prof entre, enchaine les lemmes, propositions, définitions, théorèmes et démonstrations au tableau, c'est absolument pas efficace, a la fin personne comprend rien

Il faut enseigner les théories en 3 niveaux, le prof commence par une première lecture d'une version light du cours, ou il ne présente que les définitions entières, pour limiter les contours de la théorie et si possible une représentation visuelle des objets liés aux définitions.
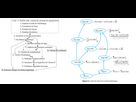
Ensuite il présente que les grands théorèmes qui sont la finalité de la théorie et les explique et leurs implication et utilité, et utilité pratique en sciences. Ensuite il approfondit avec les énoncés secondaires comme les propositions, ensuite il présente la carte mentale du cours, comment chaque proposition est connectée aux autres, telle proposition sert a démontrer quoi, et quel est l'enchainement mental pour arriver au théorème, genre avec une case avec le nom du théorème, et plein de cases connectées portant le nom des proposition/définitions avec des flèches pour suivre l'enchainement. Tout ca peut se faire en une seule séance et a une efficacité monumentale.

Puis les séances suivantes il fait le cours standard en démontrant chaque chose en détail dans l'enchainement de la carte mentale

Groupe ca doit être au minimum introduit par un groupe de matrices , comme ca au moins c'est déjà une représentation linéaire de groupes plus intéressants et exhibe des symétries, et ca a relation avec des transformations géométriques sur R3 genre rotations SO(3)

Tu y penses avant tout en te mettant à la place des élèves de L1 ou avant tout pour rendre honneur à la notion de groupe telle que tu la comprends actuellement ?

Parler de groupes de matrices nécessite déjà du matériel algébrique externe à la théorie des groupes. Rien d'insurmontable, je suis d'accord, mais rien que le fait que AB=I implique BA=I pour les matrices carrées, c'est un truc bien subtil quand même.

Le groupe symétrique est pour moi tangible lui aussi : on permute n objets. Il est naturel à considérer. Par exemple on peut penser à un paquet de cartes. Ce groupe est universel : on apprendra un jour que tout groupe de taille n se réalise dans le groupe fini Sym(n). Il faut travailler un peu pour comprendre le groupe symétrique mais là, le travail est 100% théorie des groupes. Il ne relève pas d'autres branches potentiellement d'un cours d'algèbre. On peut y étudier à la main de façon concrète des concepts qui seront généralisés plus tard (par exemple la décomposition d'une permutation en cycles à support disjoint préfigure la partition en orbites). Et on sera amené à rencontrer le groupe alterné et la signature, qui serviront à définir le déterminant.

Si seulement le prof pouvait faire des trucs comme ca, mais en plus détaillé pour chaque cours au niveau connexion entre théorèmes, définition et propositions

Oui le groupe symétrique c'est bien aussi, mais pour les élèves qui vont aussi faire de la physique, les groupes de matrices c'est le must absolu

Pour les intégrales Lebesgue, personne comprend a quoi ca sert, alors qu'il suffisait d'introduire en montrant les limitations Riemann en proposant d'intégrer l'indicatrice sur l'ensemble Q pour exemple

Le 06 juillet 2025 à 01:20:51 :
Aussi, les scénarios ou le prof entre, enchaine les lemmes, propositions, définitions, théorèmes et démonstrations au tableau, c'est absolument pas efficace, a la fin personne comprend rien

Il faut enseigner les théories en 3 niveaux, le prof commence par une première lecture d'une version light du cours, ou il ne présente que les définitions entières, pour limiter les contours de la théorie et si possible une représentation visuelle des objets liés aux définitions.
Ensuite il présente que les grands théorèmes qui sont la finalité de la théorie et les explique et leurs implication et utilité, et utilité pratique en sciences. Ensuite il approfondit avec les énoncés secondaires comme les propositions, ensuite il présente la carte mentale du cours, comment chaque proposition est connectée aux autres, telle proposition sert a démontrer quoi, et quel est l'enchainement mental pour arriver au théorème, genre avec une case avec le nom du théorème, et plein de cases connectées portant le nom des proposition/définitions avec des flèches pour suivre l'enchainement. Tout ca peut se faire en une seule séance et a une efficacité monumentale.

Puis les séances suivantes il fait le cours standard en démontrant chaque chose en détail dans l'enchainement de la carte mentale

Tu as des idées assez tranchées. C'est intéressant.

As-tu des éléments au-delà de tes convictions propres permettant de se faire une idée précise de l'efficacité avérée ou non de ces méthodes ? Autrement dit, ton propos relève-t-il plutôt de l'intime conviction ou de la méthode expérimentalement confirmée ? Si c'est le premier cas, ce n'est évidemment pas du tout un problème. Je demande seulement pour clarifier dans ma tête le statut de tes propositions (et parce que, dans le second cas, je serais intéressé par les ressources afférentes)

Le rapport avec ce que tu dis est relativement marginal mais, puisque j'y pense, je vais à mon tour partager une pensée portant sur l'enseignement.

J'ai l'impression qu'un exemple de situation qui a ses nuances de gris, c'est le "manipuler sans comprendre". Il me semble qu'il est trop simpliste de considérer que c'est évidemment OK, et trop simpliste de considérer que c'est aberrant. Spontanément, je suis team "c'est pas bien". Toutefois, il ne faut pas perdre de vue que c'est souvent en manipulant qu'on se forge une familiarité avec des objets. On peut perdre nos étudiants à parler excessivement du sens de ce qu'on fait et à ne pas suffisamment faire.

De manière générale, une pratique qui me semble contribuer à améliorer la qualité de l'enseignement, c'est de discuter avec nos étudiants de comment ils perçoivent l'enseignement, ce qui passe ou ne passe pas, etc. Prendre pour aiguillon la réalité plutôt que les principes.