Célestin veut devenir MATHEMATICIEN

Vous travaillez pendant des années. Au moment où l'épisode s'achève (fin août 2062), vous comprenez beaucoup de choses en profondeur sur l'hypothèse de Riemann généralisée mais n'avez résolu ni l'hypothèse de Riemann généralisée, ni l'hypothèse de Riemann "vanilla"

Vous êtes sceptiques sur votre capacité à résoudre ces problèmes mais vous avez déjà sous le coude des résultats partiels très impressionnants, que vous gardez confidentiels pour le moment

Vous vous donnez encore 8 mois pour obtenir les résultats les plus fins possibles, puis 14 mois pour finir de les rédiger. Cela sera pile dans les temps pour la médaille Fields de 2066, la dernière qu'Alessandra pourra espérer remporter, compte tenu de la limite d'âge de 40 ans

En effet, pour qu'une médaille Fields soit décernée à l'instant T, il faut que cela soit décidé un certain temps en amont. Vous avez calculé votre planning pour qu'à cet instant-ci, les experts mondiaux aient eu suffisamment le temps de lire vos travaux pour s'accorder sur leur valeur.

L'épisode post-Hodge s'achève ici : vous pouvez désormais voter

Exemples de votes :

Célib - 1 - 0€ - 50%
Lily - 2 - 40 000 € - 30%
Marie - 1 - 250 000 € - 40%

RAPPEL : Les votes argumentés comptent doubles
Pour qu'un vote soit argumenté, il suffit d'écrire au moins trois phrases expliquant le pourquoi de son vote

La clôture des votes aura lieu au plus tôt le mercredi 11 décembre à 22h

Le 05 décembre 2024 à 23:54:18 :
Cette sweet de qualité.

Ravi que tu apprécies

Est-ce qu'on a le prix Nevanlinna/Abacus (d'ailleurs pourquoi ils ont changé le nom ?) ?

Non, on n'a pas ce prix (notre contribution retentissante n'est pas du côté informatique des maths). Aucune idée du pourquoi derrière le changement de nom

Lily parce que sur le déclin il faut revenir vers sa jeunesse avec nostalgie (en plus ça permet une jolie boucle de fic).

2/, parce que zut à la fin, c'est sympa la vie en montagne mais il faut profiter de la vie tout de même, et puis on se fait vieux donc autant avoir du confort pour nous permettre de décliner tranquillement, pouvoir organiser des petits colloques chez soi c'est un luxe pour une personne âgée.

100K (si on part du principe que c'est en euros constants d'aujourd'hui), ça permet de faire un emprunt pour une belle maison à la campagne ou à l'étranger, faire des travaux et/ou financer quelques voyages sympathiques sans que ça mettre notre progéniture en incapacité d'améliorer sa situation par son travail.

30 %, parce qu'on est pas des radins, qu'on est déjà dans une situation matérielle confortable et que ça fait vraiment vieux pingre, comme on en voit malheureusement de temps à temps dans le monde de la recherche, de tenter de prendre une bonne partie du prestige/argent d'un prix d'un jeune chercheur qui n'a pas forcément nos appuis dans le monde académique.

Le 06 décembre 2024 à 15:39:19 :

Le 05 décembre 2024 à 23:54:18 :
Cette sweet de qualité.

Ravi que tu apprécies

Est-ce qu'on a le prix Nevanlinna/Abacus (d'ailleurs pourquoi ils ont changé le nom ?) ?

Non, on n'a pas ce prix (notre contribution retentissante n'est pas du côté informatique des maths). Aucune idée du pourquoi derrière le changement de nom

J'ai cherché sur le Wikipedia anglais, en fait Nevanlinna avait soutenu de façon un peu véhémente le H. durant la Seconde Guerre Mondiale.

Je recopie ici l'info en bas de la page précédente pour que ce soit plus mis en valeur : le prochain épisode couvrira une période de 15 ans

100K (si on part du principe que c'est en euros constants d'aujourd'hui)

Oui, on part du principe euro constant d'aujourd'hui

J'ai cherché sur le Wikipedia anglais, en fait Nevanlinna avait soutenu de façon un peu véhémente le H. durant la Seconde Guerre Mondiale.

Merci pour ton vote aussi prompt qu'étayé

Excellente sweet. Malheureusement on sent la fin de la fic approcher
Enzo le reptilien qui n'a pas vielli en 30 ans, on en parle ?

Quand la fic s'achèvera, le manque nous fera désirer un spin-off

Je le savais bon sang, toutes. Célestin n'aurait pas dû se retenir pour sa famille, j'espère qu'il retiendra la leçon.

Capucine effectue ses études à l'INSP puis devient diplomate, exerçant au consulat général de la France à Rio de Janeiro. Elle a eu le bon goût de se marier à un ingénieur disposé à la suivre où qu'elle aille et, le 18 avril 2062, te donne une petite-fille, Hypatie, que vous surnommez affectueusement Patty

, et en plus elle fait une publication en mathématiques, Capucine est excusée pour sa trahison.
Lily n'a pas pris une ride en 40 ans. En plus = LambdaDelta, soit un excellent perso d'Umineko. Bref, autant de raisons de se mettre en couple avec elle (en la faisant passer après les maths évidemment).
Autant profiter de l'offre proposée par Alessandra, je ne vois pas l'intérêt de faire preuve de modestie par pur mimétisme.
Lily - 2 - 20 000€ - 40%

Le 12 décembre 2024 à 00:21:09 :
Je le savais bon sang, toutes. Célestin n'aurait pas dû se retenir pour sa famille, j'espère qu'il retiendra la leçon.

Capucine effectue ses études à l'INSP puis devient diplomate, exerçant au consulat général de la France à Rio de Janeiro. Elle a eu le bon goût de se marier à un ingénieur disposé à la suivre où qu'elle aille et, le 18 avril 2062, te donne une petite-fille, Hypatie, que vous surnommez affectueusement Patty

, et en plus elle fait une publication en mathématiques, Capucine est excusée pour sa trahison.
Lily n'a pas pris une ride en 40 ans. En plus = LambdaDelta, soit un excellent perso d'Umineko. Bref, autant de raisons de se mettre en couple avec elle (en la faisant passer après les maths évidemment).
Autant profiter de l'offre proposée par Alessandra, je ne vois pas l'intérêt de faire preuve de modestie par pur mimétisme.
Lily - 2 - 20 000€ - 40%

Si j'y arrive (pas gagné), je ferai un sticker de Lily vieille. En espérant que ton vote ne dépende pas de ça de manière cruciale.

Les votes sont clôturés

Lily 2 100k 30%

La sweet arrivera progressivement dans les jours qui viennent

Comme d'habitude, ne pas voter tant qu'il n'est pas indiqué que vous pouvez le faire. Alors seulement l'épisode est clos

ÉPISODE RIEMANN

Dans les Hautes Sphères...

- J'ai entendu un truc, je crois

- T'es sure ?

- Oui

- Ah bah tiens, tu vois

- Bonjour

- Mais qu'est-ce que quelqu'un fout ici ?

- Décline ton identité

Jusqu'à mars 2063, Alessandra et toi bossez dur pour obtenir une version renforcée de votre théorème. Puis vous bûchez sévère pour faire converger la rédaction dans les temps prévus. Finalement, début juillet 2064, votre article est prêt mais vous attendez quelques semaines encore avant de le mettre sur arxiv

En effet, comme pour Hodge, tu as fait organiser par un complice une conférence sur l'hypothèse de Riemann et des thèmes voisins, pour fin juillet. La conférence dure une semaine, du lundi au vendredi. Histoire de ne pas être trop grillé par mimétisme avec Hodge, Alessandra et toi ne vous mettez pas sur les tous premiers créneaux de la conf mais en début d'après-midi du lundi

C'est Alessandra qui donne le premier exposé et qui annonce d'emblée votre percée sur l'hypothèse de Riemann généralisée, ce qui ne manque pas de faire réagir dans la salle

Elle expose dans les très grandes lignes la structure de la démonstration. Puis, dans ton exposé, tu donnes une vue légèrement plus détaillée des arguments à l'oeuvre

La saveur de déjà vu entre cet événement et Hodge semble susciter par elle-même pas mal d'excitation, qui prend généralement la forme de hype mais parfois d'agacement ou d'irritabilité. L'ambiance est particulière mais à nouveau, ce qui domine est l'appétit vorace d'en savoir plus sur cette contribution majeure

La majeure partie des orateurs annule spontanément ses exposés pour vous permettre de donner plus de détails. Certains autres le font car ils s'y sentent obligés par pression des pairs. Et quelques uns maintiennent leurs exposés. Une partie du public vous propose de faire en session parallèle des exposés sur vos travaux, ce à quoi vous vous refusez, par respect pour les autres orateurs. Vous assistez avec attention à leurs exposés et essayez de poser des questions en fin d'exposé pour témoigner votre intérêt pour leurs travaux. D'autres exposés encore sont annulés car rendus caduques par vos travaux

Jusque là, tu n'avais pas capté que ce genre de mise en scène, que ce soit pour Hodge ou en ce moment pour Riemann, était moyennement respectueuse des autres orateurs invités. Tu perçois concrètement la frustration que ça peut engendrer aujourd'hui : est-ce parce que tu perçois mieux les choses ou parce que l'ambiance était différente du temps de Hodge ?

Votre preprint Generalized Riemann Hypothesis almost holds for almost every Dirichlet L-function paraît sur arxiv le mardi. Finalement, votre contribution tient en 87 pages bien tassées. Capucine figure dans les remerciements : à l'un de ses passages à Paris, vous discutiez le soir de certains problèmes techniques et les pistes qu'elle vous a proposées vous ont probablement fait gagner 1 ou 2 mois et raccourci le papier de 2-3 pages

Jusqu'à mars 2063, Alessandra et toi bossez dur pour obtenir une version renforcée de votre théorème. Puis vous bûchez sévère pour faire converger la rédaction dans les temps prévus. Finalement, début juillet 2064, votre article est prêt mais vous attendez quelques semaines encore avant de le mettre sur arxiv

En effet, comme pour Hodge, tu as fait organiser par un complice une conférence sur l'hypothèse de Riemann et des thèmes voisins, pour fin juillet. La conférence dure une semaine, du lundi au vendredi. Histoire de ne pas être trop grillé par mimétisme avec Hodge, Alessandra et toi ne vous mettez pas sur les tous premiers créneaux de la conf mais en début d'après-midi du lundi

C'est Alessandra qui donne le premier exposé et qui annonce d'emblée votre percée sur l'hypothèse de Riemann généralisée, ce qui ne manque pas de faire réagir dans la salle

Elle expose dans les très grandes lignes la structure de la démonstration. Puis, dans ton exposé, tu donnes une vue légèrement plus détaillée des arguments à l'oeuvre

La saveur de déjà vu entre cet événement et Hodge semble susciter par elle-même pas mal d'excitation, qui prend généralement la forme de hype mais parfois d'agacement ou d'irritabilité. L'ambiance est particulière mais à nouveau, ce qui domine est l'appétit vorace d'en savoir plus sur cette contribution majeure

La majeure partie des orateurs annule spontanément ses exposés pour vous permettre de donner plus de détails. Certains autres le font car ils s'y sentent obligés par pression des pairs. Et quelques uns maintiennent leurs exposés. Une partie du public vous propose de faire en session parallèle des exposés sur vos travaux, ce à quoi vous vous refusez, par respect pour les autres orateurs. Vous assistez avec attention à leurs exposés et essayez de poser des questions en fin d'exposé pour témoigner votre intérêt pour leurs travaux. D'autres exposés encore sont annulés car rendus caduques par vos travaux

Jusque là, tu n'avais pas capté que ce genre de mise en scène, que ce soit pour Hodge ou en ce moment pour Riemann, était moyennement respectueuse des autres orateurs invités. Tu perçois concrètement la frustration que ça peut engendrer aujourd'hui : est-ce parce que tu perçois mieux les choses ou parce que l'ambiance était différente du temps de Hodge ?

Votre preprint Generalized Riemann Hypothesis almost holds for almost every Dirichlet L-function paraît sur arxiv le mardi. Finalement, votre contribution tient en 87 pages bien tassées. Capucine figure dans les remerciements : à l'un de ses passages à Paris, vous discutiez le soir de certains problèmes techniques et les pistes qu'elle vous a proposées vous ont probablement fait gagner 1 mois et raccourci le papier de 2-3 pages

8 août 2064

Tu as une grosse journée derrière toi et t'es crevé, mais Alessandra passe au journal télévisé alors tu luttes contre le sommeil pour écouter son entretien.

- Madame Banador, bonsoir

- Bonsoir

- Vous êtes chercheuse en mathématiques au CNRS et avez récemment obtenu des progrès fulgurants sur l'hypothèse de Riemann. Pouvez-vous nous en dire plus ?

- Tiens, ça sera plus marrant si les explications viennent de Fred et Jamy

- Euh, t'as le droit de changer le monde impunément, toi ?

- Eh oui, Narrateur, le Patron est tout-puis-sant

- Mais alors, Jamy, qu'est-ce que l'hypothèse de Riemann ?

- Eh bien si tu parles anglais, écoute 3blue1brown
https://www.youtube.com/watch?v=sD0NjbwqlYw

- Et si tu fais ton taf au lieu de déléguer, ça donne quoi Jamy ?

- Avant cela, permets-moi de te présenter...

- Mon fils

- Ma femme

- Mon chien

- Mais dis-moi, Jamy, aurais-tu recommencé le L S D ?

- P-pas du tout, Fred, voici les explications

- Depuis l'Antiquité, les mathématiciens essaient d'étudier les propriétés fines des nombres entiers. C'est un sujet mathématiquement fascinant, qui de plus se trouve lié à bien d'autres sujets à travers les mathématiques et les sciences, comme l'informatique ou même la physique, Fred

- Et l'hypothèse de Riemann, dans tout ça ?

- Dans ses recherches sur les nombres premiers, Riemann a introduit un nuage de points dans le plan. Pour les mathématiciens postérieurs à Riemann, définir ce nuage de points n'est pas difficile, mais l'étudier est com-pli-qué

- On a une bande, là, avec une droite au milieu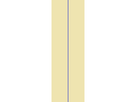

- En dehors de la bande, on comprend globalement bien ce qui se passe : il n'y a aucun point de notre nuage à droite de la bande et ceux à gauche sont tous sur cette droite horizontale, en rouge

- Mais dans la bande, alors, que se passe-t-il, Jamy ?

- Excellente question, Fred

- Riemann avait de bonnes raisons de penser qu'ils doivent tous être sur cette droite bleue là, pile au milieu de la bande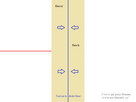

- Si tel est bien le cas, on peut en déduire de nombreuses conséquences sur les nombres entiers ou sur d'autres situations mathématiques

- Et alors, Jamy, Riemann avait-il raison ?

- On n'en sait rien, Fred. Cet énoncé s'appelle l'hypothèse de Riemann et c'est un Graal des mathématiques. Il fait partie des 23 problèmes de Hilbert, une liste de problèmes que le mathématicien Hilbert a détaché comme cruciaux en 1900. C'est aussi le premier des 18 problèmes de Smale, liste réalisée en 2000, ainsi que l'un des sept problèmes du Millénaire

- Savait-on des choses à ce sujet, avant les contributions d'Alessandra Banador et Célestin Chancla ?

- On sait de longue date qu'il n'y a pas de point de notre nuage situé pile poil sur les droites qui délimitent les bords gauche et droit de la bande. Et rien que ça, ça a permis, en 1896, aux mathématiciens Hadamard et de La Vallée Poussin de démontrer, chacun de son côté, le "théorème des nombres premiers"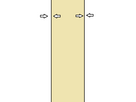

- Mais quel est ce théorème ?

- Il nous donne une bonne estimation du nombre de nombres premiers plus petits qu'un entier N donné. Si on fait le ratio entre le vrai décompte et la formule simple du théorème des nombres premiers, ça converge vers 1

- Si on arrive à s'assurer qu'aucun point ne s'approche trop des bords de la bande, on peut contrôler de façon plus fine encore l'erreur commise dans ce théorème. Et si tous les points sont sur la ligne bleue centrale, alors ça dit que la formule fournit une excellente approximation

- Mais alors, qu'ont démontré Alessandra Banador et Célestin Chancla ?

- Avant d'en arriver là, il faut parler de l'hypothèse de Riemann généralisée : au lieu d'étudier un seul nuage de points, on en considère une infinité. On ne va pas s'amuser à les superposer : chaque nuage de points a son propre dessin

- Pour chacun de ces dessins, en dehors de la bande, tout est globalement bien compris : il n'y a aucun point à droite et, sur la gauche, ils sont tous bien compris. Mais dans la bande : mystère ! L'hypothèse de Riemann généralisée prédit que, à chaque fois, tous les points tombent pile poil sur la droite verticale bleue, bien au centre de la bande

- La bande beige est bien la même pour tous les dessins, d'ailleurs : elle a la même largeur à chaque fois et est positionnée au même endroit

- Et alors, c'est pas qu'on s'emmerde mais quelle est la contribution de Banador et Chancla ?

- Ils n'étudient pas l'hypothèse de Riemann mais la version plus générale encore : l'hypothèse de Riemann généralisée. Ils disent qu'un dessin vérifie presque l'hypothèse de Riemann si, à chaque fois qu'on prend une bande verticale cyan centrée sur la droite bleue, il n'y a qu'un nombre fini de points du nuage qui se trouve dans la zone beige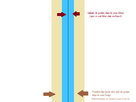

- S'ils démontraient que ce nombre est nul au lieu d'être fini, ça reviendrait à dire que le dessin étudié vérifie l'hypothèse de Riemann. D'où la dénomination "presque vérifier l'hypothèse de Riemann"

- Et donc ils démontrent que chaque nuage de points vérifie presque l'hypothèse de Riemann

- Non... ils démontrent presque ça : ils démontrent que "presque tout nuage vérifie presque l'hypothèse de Riemann"

- Ca ne veut rien dire, Jamy : quel est le sens à donner à cette phrase ?

- Ils démontrent qu'il n'y a qu'un nombre fini de nuages de points qui ne vérifient pas presque l'hypothèse de Riemann. Autrement dit, l'ensemble des nuages de points qui ne vérifient pas presque l'hypothèse de Riemann est fini

- Oulalah, c'est incompréhensible cette histoire

- Parce que les non-mathématiciens sont peu habitués à ce genre de nuances, avec des énoncés très précis à rallonge. Pour les mathématiciens, inversement, c'est une banalité de parler comme cela. Par exemple, Banador et Chancla ont bossé 8 mois supplémentaires pour améliorer leur énoncé, passant d'un énoncé plus faible à l'énoncé actuel

- Quel était cet énoncé faible ?

- "Pour toute bande cyan autour de la droite bleue, il n'y a qu'un nombre fini de nuages qui ont une infinité de points dans la zone beige"

- Quoi ? C'est pas le même énoncé ?

- Non, l'ordre dans lequel on introduit les protagonistes n'est pas le même. C’est le genre de subtilités dont on a peu conscience dans le langage courant mais qui joue un rôle crucial dans les maths de l'éducation supérieure et de la recherche. Dans ce cas précis, pour l'énoncé faible, on peut imaginer que si la bande cyan est de largeur 1/10, il y a 20 nuages pour qui ça se passe mal, que pour une largeur 1/100 il y en a 1500, que pour une largeur 1/1000 il y en a 800 000... Alors qu'avec l'énoncé final, on peut trouver une même valeur qui fonctionne pour toutes les bandes : du genre, quelle que soit la largeur choisie, il y a au plus 17 000 nuages pour qui ça se passe mal

- Si tu le dis. Et 17 000 est-elle la valeur correcte, Jamy ?

- On n'en sait rien, Fred : on sait que ce nombre existe mais on n'a aucune idée de sa valeur. On dit que la démonstration est non-constructive. Elle fait intervenir une notion mathématique appelée "compacité", qui déborde largement du cadre de ces explications

- Et donc ça dit quoi sur l'hypothèse de Riemann elle-même ?

- Absolument rien, Fred ! Ce nuage pourrait très bien être l'une des exceptions, auquel cas le théorème ne nous dit rien dessus

- Mais attends, Jamy, ta remarque s'applique aussi aux autres nuages de points : en définitive, leur théorème ne dit rien du tout

- Effectivement, Fred, le théorème ne dit rien de concret. Sur chaque nuage pris isolément, on ne peut rien dire. Toutefois, le théorème de Banador-Chancla donne de précieuses informations sur le comportement collectif des nuages quand on les considère tous ensemble : on ne sait pas localiser quelles sont les situations mauvaises mais on sait abstraitement qu’elles sont très minoritaires ! C'est une contribution majeure sur le sujet. En comparaison, les travaux effectués depuis Riemann sur le sujet ne faisaient que gratter la surface : on ne savait même pas montrer qu'il existe un nuage pour lequel on puisse trouver une bande cyan légèrement plus étroite telle qu'aucun point ne tombe dans la zone beige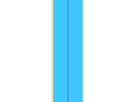

- Ah bon, on ne savait pas ça ? Pourtant, ne sait-on pas qu'il n'y a aucun point pile sur les bords de la bande ?

- Tout à fait mais on pourrait imaginer qu'il y ait des points qui approchent le bord comme sur cette figure. En montant très très haut dans la bande, on pourrait alors trouver des points très proches du bord, sortant donc de notre bande cyan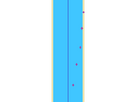

- Si tu le dis. Et cet énoncé qui nous échappait avant, là, celui dont tu viens de parler avec la bande cyan légèrement plus étroite, on sait le démontrer maintenant ?

- Oui, et même beaucoup mieux ! Il découle du théorème de Banador-Chancla (et même de sa version faible) que cette propriété est vérifiée par presque tous les nuages : tous les nuages sauf un nombre fini (conjecturalement nul) d'entre eux vérifient cette propriété

- Et donc, Jamy, où en sommes-nous ?

- Avant Banador-Chancla, on avait le sentiment de gratter la surface. Désormais, nous sommes encore loin de la destination mais on a l'impression d'avoir effectué une partie du trajet

- Chéri, réveille-toi

Jet de romance Lily : https://youtu.be/CiEhBDO6VpE

- Ah zut, le journal est terminé. J’ai fait un rêve bizarre sur comment vulgariser mes travaux, attends, je vais prendre des notes, c’était pas mal

Tu crois avoir aperçu un ou deux autres personnages que les vulgarisateurs mais tu ne parviens pas à ressaisir ce souvenir de rêve qui s’est définitivement évaporé

L'été il y a deux ans, tu as revu Lily. Tantôt une semaine dans tes montagnes, tantôt à Oxford où elle est professeur d'université. Vous vous êtes remis ensemble. Vous vous voyez lorsque vous en avez le temps et l'envie, sans vous prendre la tête. Ca fonctionne bien globalement. Vous n'êtes plus des enfants, vous abordez les choses avec pragmatisme et n'avez pas envie de vous monter le bourrichon

Ce n'est pas un amour fou et exubérant, plutôt deux personnes qui ont un passé commun et qui apprécient se tenir compagnie et partager de l'intimité

Bref, reprenons : tu es au milieu de la tempête Riemann

Vous aviez convenu avec Alessandra un pourcentage de 70% en sa faveur. C'est ce qui te paraît juste quand tu resonges à la situation symétrique que tu as elle aussi vécue. Là, finalement, puisque vous n'avez pas résolu Riemann, seulement avancé sur le problème, la question ne concerne pas le prix du Millénaire mais la répartition des autres prix. Mais comme il ne te manque pas grand chose côté prix, avec ce quota de 30%, tu reçois, au fil des années qui viennent, tous les prix possibles : tu n'auras pas la médaille Fields (contrainte d'âge) ni les prix qui ont des limites thématiques, géographiques ou autres qui t'excluent, mais à part ça, tu collectes tous les pins qui manquaient à ta collec

En janvier 2066, votre article a été relu et approuvé et paraît au journal Annals of Mathematics. Et c'est sans surprise qu'Alessandra reçoit la médaille Fields six mois plus tard

Le lendemain, succès unlocked : spaghettis de Lorenzo Banador

Alessandra rejoint le Collège de France, chaire de Théorie des Nombres

En ce qui te concerne, Lily vient vivre en France à tes côtés : elle vient de prendre sa retraite d'Oxford. Quant à toi, tu décides de continuer de remplir tes fonctions de professeur jusqu'à tes 70 ans. L'occasion de continuer d'accumuler un très confortable pécule : avec ton salaire francosuisse et les prix que tu reçois, ta fortune continue de monter

Une fois retraité (avec un statut de professeur émérite à l'EPFL et de professeur honoraire au collège de France), tu continues de faire des maths, depuis tes montagnes. Quand tu veux collaborer, tu fais venir tes collaborateurs que tu peux loger de façon très classe dans tes dépendances

Car oui, fort de tes richesses, tu disposes d'un immense terrain près de Chambéry où tu as fait bâtir et aménager diverses dépendances. Tu as, sur le même terrain, une grande et vieille maison traditionnelle, une grande maison très moderne, un superbe jardin et un complexe de conférences pour 15 personnes : logement, salles de travail, salle de conf

Des tableaux noirs se trouvent un peu partout, en intérieur comme en extérieur

Tu fais toi-même ce qui te plait mais as les moyens d'employer du personnel qualifié pour toute tâche que tu préfères déléguer. Tu as aussi un appartement à Paris. Jusqu'à tes 70 ans, il te servait pour tes passages à Paris et pour dépanner famille et collègues : tu le louais dans ce cas à un tarif défiant toute concurrence, cherchant seulement à ce que la possession de ce bien ne fasse pas décroître ton compte en banque (tu fais payer les charges de copropriété, la taxe d'habitation, l'eau et l'électricité). Une fois retraité, tu n'es pas contre une petite rente et mets en location cet appartement au prix du marché

Après Riemann, tu n'as pas eu de difficulté à continuer de faire des maths. Mais, de ce moment-ci jusqu'à la fin de l'épisode (août 2077), ta production est celle d'un professeur d'universités normal : elle ne se dégage pas comme exceptionnelle

Les anciens viennent à mourir : Cussec en 64, Kovacs et Kilton en 70