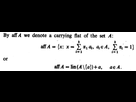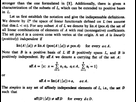[MATHS] C'est vraiment EGAL ?

Le 28 octobre 2021 à 02:29:27 :
Franchement la flemme là en plus la qualité est dégueu

Certes mais c'est tout à fait lisible. De toutes façons j'ai pas l'impression qu'il y ait grand chose à comprendre, il a visiblement défini deux trucs différents avec la même notation.

Effectivement c'est étrange, si A={(1,0);(0,1)} alors aff(A) est la droite d'équation y=-x+1 mais lin(A\(0,1))+(0,1) est la droite d'équation y=1 et lin(A\(1,0))+(1,0) est la droite d'équation x=1

...

Ok j'ai réfléchi et je crois que j'ai trouvé, en fait on a aff(A)= lin(A-a)+a, et ce quel que soit le point a de A. Je parie sur un éditeur trop zélé qui a du modifier le A-a en A\{a} sans comprendre que ça ne voulait pas du tout dire la même chose ici

Le 28 octobre 2021 à 13:16:59 :
Effectivement c'est étrange, si A={(1,0);(0,1)} alors aff(A) est la droite d'équation y=-x+1 mais lin(A\(0,1))+(0,1) est la droite d'équation y=1 et lin(A\(1,0))+(1,0) est la droite d'équation x=1

...

Ok j'ai réfléchi et je crois que j'ai trouvé, en fait on a aff(A)= lin(A-a)+a, et ce quel que soit le point a de A. Je parie sur un éditeur trop zélé qui a du modifier le A-a en A\{a} sans comprendre que ça ne voulait pas du tout dire la même chose ici

Merci khey !
On est vraiment sur le forum de l'élite !

Le 28 octobre 2021 à 13:25:50 :
Il y a clairement un abus de notation sur la deuxième ligne. Si on considère que c'est union {a}, ça ne me dérange pas.

Même avec "union A" les deux définitions ne seraient pas équivalentes, mais la proposition de jeancommutatif semble très bien fonctionner