[MATH] Cette démonstration TOURNEBOULE le forum

Je vous remet un peu dans le contexte :Pour ceux qui ont la flemme de lire le pavé la démo est ici

Vous êtes en MP* d'une bonne prépa et parmi les meilleurs de votre promo, les Cassinis sont sus, les Gourdons maitrisés. Votre prof de math vous a donné un DM sur les séries de fonctions, il s'agit d'un vieux sujet de l'X : fonction zeta de Riemann et transformée de Melin au programme, ça s'annonce intéressant.

Comme Caboche (c'est le surnom de votre prof) est fainéant et n'aime pas corriger de copies ils vous demande de faire le DM à 2, vous le faite donc avec Bactopin https://www.delcourt.fr/3023-large_default/Detergent-desinfectant-BACTOPIN-S-750-ml.jpg , votre pote depuis le collège. Le problème c'est que Bactopin n'a pas votre talent, il minore constamment les DS et la rumeur court que s'il est en étoile c'est juste parce que son oncle est l'ami d'enfance du directeur de la prépa

Vous décidez donc de lui laisser la partie A pendant que vous vous occuperez des 6 suivantes, vous vous dites que ça devrait être à sa portée, c'est niveau sup après tout. Vous vous installez donc tous deux à la bibliothèque prêts à bosser tranquillement le dm, malheureusement au bout de 10 minutes vous sentez bactopin s'agiter sur sa chaise, il semble nerveux et mal à l'aise, il finit par vous demander :
-Dis <tonpseudo> je bloque sur la question A.I.1.1.b tu te rappelles comment on fait pour montrer que la série des 1/n diverge ? Je sais qu'on l'a vu en sup mais j'ai un trou... Il faut faire une démonstration par l'absurde c'est ça ?
Vous soupirez intérieurement, entre la sommation par paquets, le critère de Cauchy et la comparaison série/intégrale vous voyez une demi douzaine de façon de le démonter mais aucune n'utilise de raisonnement pas l'absurde. Mais vous n'allez pas faire le DM tout seul, c'est votre pote d'accord mais qu'il se débrouille tout seul avec sa question de CCP !
-Heu je sais plus trop... ouais ouais tu peux essayer ça si tu veux...
Un quart d'heure plus tard bactopin tout content vous annonce qu'il vient de retrouver la démonstration, il est même tellement fier de lui qu'il vous tend sa feuille avec un "regardes !" pour que vous jetiez un œil à sa preuve. À moitié amusé par la situation vous consentez à lire sa démonstration, persuadé de bien vous marrer devant une bouillie d'inepties. En saisissant sa copie double vous y découvrez ceci :

Votre réaction ? Êtes vous tourneboulé ?

Le 26 mai 2021 à 22:06:56 :
Bactopin majorera l'X cette année

Probable

Démontrer que tout nombre rationnel est la somme des cubes de trois nombres rationnels.

Solution :

Si vous avez d'autres démonstrations tourneboulantes n'hésitez pas à les poster

Je referais certainement ce topic parce que je me suis un peut trop emballé pour le contexte et mon pavé est bien trop long

Le 26 mai 2021 à 22:11:09 :
Démontrer que tout nombre rationnel est la somme des cubes de trois nombres rationnels.

Solution :

Ca se trouve de tête ça

Le 26 mai 2021 à 22:12:25 :
Si vous avez d'autres démonstrations tourneboulantes n'hésitez pas à les poster

Je referais certainement ce topic parce que je me suis un peut trop emballé pour le contexte et mon pavé est bien trop long

Je viens d'en poster une, juste au-dessus

Soit un train se déplaçant d'un point A à un point B à la vitesse de 10 km/h.
La distance entre A et B est de 10 km.
Soit une mouche qui part de B et qui fait des allers-retours entre le point B et le train.
Cette mouche va à la vitesse constante de 60 km/h (c'est une mouche très rapide).
Elle fait constamment des allers-retours entre le train et le point B et s'arrête dès que le train est arrivé.

Quelle distance la mouche parcourt en tout ?

La mouche va s'arrêter en même temps que le train, c'est-à-dire au bout d'une heure, donc elle aura parcouru exactement 60 km

Considérons deux carrés de coté 2 ayant le meme centre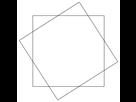

Expliquer pourquoi l'aire de leur intersection est plus grande que 3

Puisque ils ont le meme centre, ils ont en particulier le meme cercle inscrit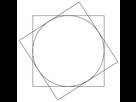

L'aire de leur intersection est alors évidemment supérieure à l'aire de ce cercle

Cercle dont l'aire vaut π > 3

CQFD

Le 26 mai 2021 à 22:14:53 :
Soit un train se déplaçant d'un point A à un point B à la vitesse de 10 km/h.
La distance entre A et B est de 10 km.
Soit une mouche qui part de B et qui fait des allers-retours entre le point B et le train.
Cette mouche va à la vitesse constante de 60 km/h (c'est une mouche très rapide).
Elle fait constamment des allers-retours entre le train et le point B et s'arrête dès que le train est arrivé.

Quelle distance la mouche parcourt en tout ?

La mouche va s'arrêter en même temps que le train, c'est-à-dire au bout d'une heure, donc elle aura parcouru exactement 60 km

Les vrais matheux calculent la série

Le 26 mai 2021 à 22:14:53 :
Soit un train se déplaçant d'un point A à un point B à la vitesse de 10 km/h.
La distance entre A et B est de 10 km.
Soit une mouche qui part de B et qui fait des allers-retours entre le point B et le train.
Cette mouche va à la vitesse constante de 60 km/h (c'est une mouche très rapide).
Elle fait constamment des allers-retours entre le train et le point B et s'arrête dès que le train est arrivé.

Quelle distance la mouche parcourt en tout ?

La mouche va s'arrêter en même temps que le train, c'est-à-dire au bout d'une heure, donc elle aura parcouru exactement 60 km

Pas vraiment une démonstration mais c'est sympathique

Le 26 mai 2021 à 22:12:47 :
Sympa pour une fois que c'est pas un truc vraiment stupide (les fameux 1=0, ce genre de trucs qu'on comprend en première)

Je ne suis pas sûr de comprendre ton analogie, le raisonnement de Bactopin est certifié correct par mon père docteur quantique, alors que les "démonstrations" de 1=0 ne sont que tromperies et esbroufe

Le 26 mai 2021 à 22:13:03 :

Le 26 mai 2021 à 22:12:25 :
Si vous avez d'autres démonstrations tourneboulantes n'hésitez pas à les poster

Je referais certainement ce topic parce que je me suis un peut trop emballé pour le contexte et mon pavé est bien trop long

Je viens d'en poster une, juste au-dessus

J'ai vu, je connaissais déjà D'ailleurs c'est peut-être de toi que je la connaissait parce que je l'ai vu pour la première fois sur ce forum.

Dans le même genre y en a une célèbre où il faut trouver un polynôme réel P tel que P^2 ait moins de coefficients non nuls que P.

- On dispose de 9 poires qui ont toutes exactement le meme poids sauf une un peu plus lourde que les autres.
- On dispose d'une balance parfaitement équilibrée

Quel est le nombre minimal de pesées à effectuer pour identifer à coup sur la poire la plus lourde ? ( Expliquer )

On fout 342 points dans un cube A de coté 7.
Existe-il un cube unité, à l'intérieur de A, qui ne contient aucun point ?

Bah oui, puisque 7^3 = 343, il y a 343 cubes unités à l'intérieur de A, 343 cubes pour 342 points, forcément yen a un qui va se retrouver vide

Prouver que si n est un entier relatif tel que n + 3 et n² + 3n + 3 sont des cubes parfaits, alors n = -2

En faisant le produit de n + 3 et n² + 3n + 3, ca nous donne n^3 + 6n² + 12n + 9.
Le produit de deux cubes étant un cube, ce truc est censé etre un cube.

Or on remarque que ce truc est en fait égal à (n+2)^3 + 1.

On a donc 2 cubes consécutifs, ca n'existe pas à part -1 et 0 ou 0 et 1.
Du coup, (n+2)^3 vaut -1 ou 0.

Du coup n = - 3 ou n = -2.

n = -3, c'est mort car (-3)² + 3*(-3) + 3 = 3 n'est pas un cube donc n = -2

Le 26 mai 2021 à 22:18:38 :

Le 26 mai 2021 à 22:12:47 :
Sympa pour une fois que c'est pas un truc vraiment stupide (les fameux 1=0, ce genre de trucs qu'on comprend en première)

Je ne suis pas sûr de comprendre ton analogie, le raisonnement de Bactopin est certifié correct par mon père docteur quantique, alors que les "démonstrations" de 1=0 ne sont que tromperies et esbroufe

Le 26 mai 2021 à 22:13:03 :

Le 26 mai 2021 à 22:12:25 :
Si vous avez d'autres démonstrations tourneboulantes n'hésitez pas à les poster

Je referais certainement ce topic parce que je me suis un peut trop emballé pour le contexte et mon pavé est bien trop long

Je viens d'en poster une, juste au-dessus

J'ai vu, je connaissais déjà D'ailleurs c'est peut-être de toi que je la connaissait parce que je l'ai vu pour la première fois sur ce forum.

Dans le même genre y en a une célèbre où il faut trouver un polynôme réel P tel que P^2 ait moins de coefficients non nuls que P.

Justement, les topics habituels sont souvent des simples tromperies grotesques

On considère le disque suivant découpé en six secteurs numérotés comme suit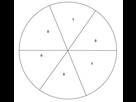

On souhaite faire en sorte qu'il y ait le meme nombre dans chaque secteur mais la seule chose qu'on ait le droit de faire autant que l'on veut, c'est choisir deux secteurs voisins et les augmenter de 1.

Peut-on arriver à obtenir le meme nombre dans chaque secteur ?

Colorons en rouge un secteur sur 2 et en bleu les autres, comme ceci :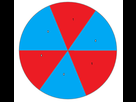

Au départ, la somme des secteurs rouges vaut 2 et celle des bleus vaut 0.
A chaque augmentation de 1 de deux secteurs voisins, l'écart entre ces deux sommes vaudra toujours 2.
Impossible donc d'arriver à avoir le meme nombre dans chaque secteur